Surabhi Luthra, Alexandra E. Moylett, Dan E. Browne, Earl T. Campbell

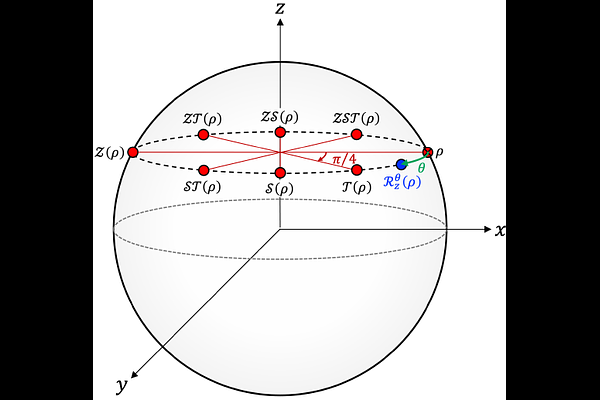
As quantum computing progresses towards the early fault-tolerant regime, quantum error correction will play a crucial role in protecting qubits and enabling logical Clifford operations. However, the number of logical qubits will initially remain limited, posing challenges for resource-intensive tasks like magic state distillation. It is therefore essential to develop efficient methods for implementing non-Clifford operations, such as small-angle rotations, to maximise the computational capabilities of devices within these constraints. In this work, we introduce mitigated magic dilution (MMD) as an approach to synthesise small-angle rotations by employing quantum error mitigation techniques to sample logical Clifford circuits given noisy encoded magic states. We explore the utility of our approach for the simulation of the 2D Fermi-Hubbard model. We identify evolution time regimes where MMD outperforms the Ross-Selinger gate synthesis method [Quantum Inf.\ Comp.\ \textbf{16}, 901-953 (2016), arXiv:1403.2975] in the number of noisy encoded magic states required for square lattices up to size $8 \times 8$. Moreover, we demonstrate that our method can provide a practical advantage which is quantified by a better-than-quadratic improvement in the resource requirements for small-angle rotations over classical simulators. This work paves the way for early fault-tolerant demonstrations on devices supporting millions of quantum operations, the so-called MegaQuOp regime.