Zhenyu Du, Yifan Tang, Andreas Elben, Ingo Roth, Jens Eisert, Zhenhuan Liu

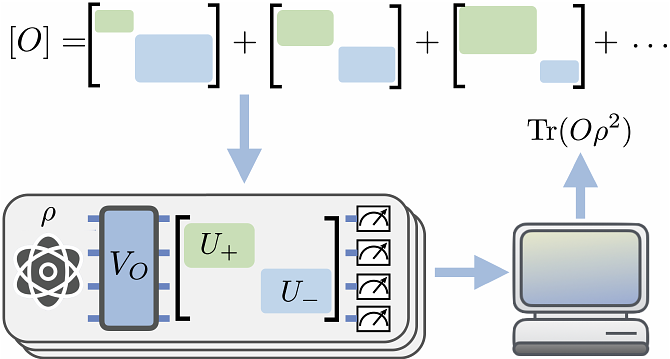
Quantum learning encounters fundamental challenges when estimating non-linear properties, owing to the inherent linearity of quantum mechanics. Although recent advances in single-copy randomized measurement protocols have achieved optimal sample complexity for specific tasks like state purity estimation, generalizing these protocols to estimate broader classes of non-linear properties without sacrificing optimality remains an open problem. In this work, we introduce the observable-driven randomized measurement (ORM) protocol enabling the estimation of ${\rm Tr}(O\rho^2)$ for an arbitrary observable $O$ -- an essential quantity in quantum computing and many-body physics. ORM achieves this by decomposing the observable $O$ into dichotomic observables and extracting the information of each eigenspace through randomized measurements with block-diagonal unitaries. We establish an upper bound for ORM's sample complexity and prove its optimality for all Pauli observables, closing a gap in the literature. Furthermore, we develop simplified variants of ORM for local Pauli observables and introduce a braiding randomized measurement protocol for fidelity estimation, both of which significantly reduce circuit complexities in practical applications. Numerical experiments validate that ORM requires substantially fewer state samples to achieve the same precision compared to classical shadows.