Colin Samplawski, Adam D. Cobb, Manoj Acharya, Ramneet Kaur, Susmit Jha

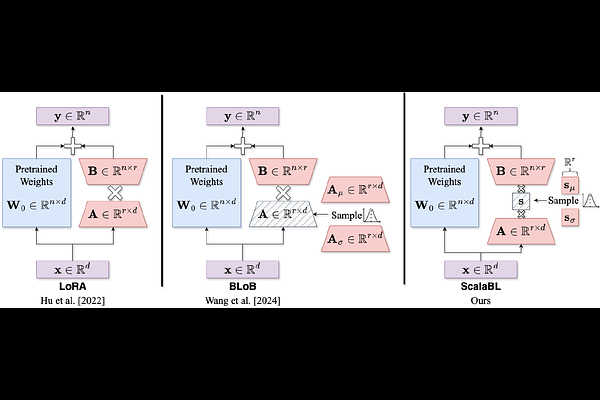
Despite their widespread use, large language models (LLMs) are known to hallucinate incorrect information and be poorly calibrated. This makes the uncertainty quantification of these models of critical importance, especially in high-stakes domains, such as autonomy and healthcare. Prior work has made Bayesian deep learning-based approaches to this problem more tractable by performing inference over the low-rank adaptation (LoRA) parameters of a fine-tuned model. While effective, these approaches struggle to scale to larger LLMs due to requiring further additional parameters compared to LoRA. In this work we present $\textbf{Scala}$ble $\textbf{B}$ayesian $\textbf{L}$ow-Rank Adaptation via Stochastic Variational Subspace Inference (ScalaBL). We perform Bayesian inference in an $r$-dimensional subspace, for LoRA rank $r$. By repurposing the LoRA parameters as projection matrices, we are able to map samples from this subspace into the full weight space of the LLM. This allows us to learn all the parameters of our approach using stochastic variational inference. Despite the low dimensionality of our subspace, we are able to achieve competitive performance with state-of-the-art approaches while only requiring ${\sim}1000$ additional parameters. Furthermore, it allows us to scale up to the largest Bayesian LLM to date, with four times as a many base parameters as prior work.