Himanshu Badhani, Dhanuja G S, Swati Choudhary, Vishal Anand, Siddhartha Das

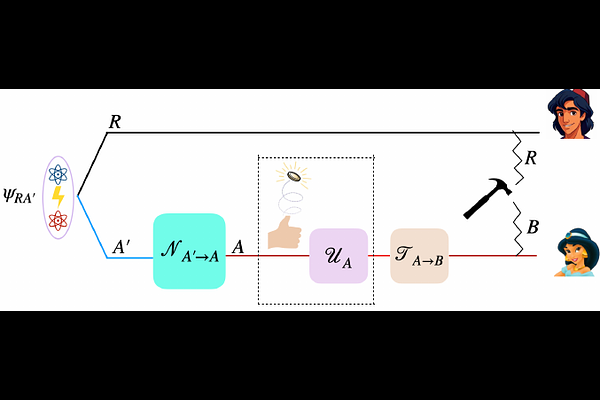
The erasure of information is fundamentally an irreversible logical operation, carrying profound consequences for the energetics of computation and information processing. In this work, we investigate the thermodynamic costs associated with erasing (and preparing) quantum processes. Specifically, we analyze an arbitrary bipartite unitary gate acting on logical and ancillary input-output systems, where the ancillary input is always initialized in the ground state. We focus on the adversarial erasure cost of the reduced dynamics~\textemdash~that is, the minimal thermodynamic work required to erase the logical output of the gate for any logical input, assuming full access to the ancilla but no access to any purifying reference of the logical input state. We determine that this adversarial erasure cost is directly proportional to the negative min-entropy of the reduced dynamics, thereby giving the dynamical min-entropy a clear operational meaning. A key foundation of this result is the quantum process decoupling theorem, which quantitatively relates the decoupling ability of a process with its min-entropy. This insight bridges thermodynamics, information theory, and the fundamental limits of quantum computation.