Kentaro Yamamoto, Yuta Kikuchi, David Amaro, Ben Criger, Silas Dilkes, Ciarán Ryan-Anderson, Andrew Tranter, Joan M. Dreiling, Dan Gresh, Cameron Foltz, Michael Mills, Steven A. Moses, Peter E. Siegfried, Maxwell D. Urmey, Justin J. Burau, Aaron Hankin, Dominic Lucchetti, John P. Gaebler, Natalie C. Brown, Brian Neyenhuis, David Muñoz Ramo

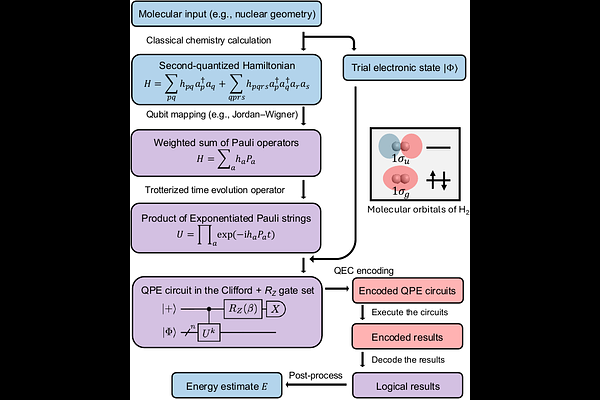
We present the first demonstration of an end-to-end pipeline with quantum error correction (QEC) for a quantum computation of the electronic structure of molecular systems. Using Quantinuum H2-2, we calculate the ground-state energy of molecular hydrogen, using quantum phase estimation (QPE) on qubits encoded with the $[[7,1,3]]$ color code. To improve on the performance of the logical compilation of the QPE circuits into the Clifford+$T$ gate set, we introduce several partially fault-tolerant (FT) techniques for the Clifford+$R_{Z}$ (arbitrary-angle single-qubit rotation) gate set. To enhance computational fidelity, we integrate Steane QEC gadgets for real-time error correction, demonstrating measurable improvements in precision. The circuits used contain 22 qubits, and up to 2185 physical two-qubit gates and $760$ mid-circuit measurements. We observe that adding QEC gadgets in the middle of circuits improves the QPE circuits' performance despite the complexity of the extra QEC circuitry. The energy $E$ is experimentally estimated to within $E - E_{\mathrm{FCI}} = 0.018(10)$ hartree, where $E_{\mathrm{FCI}}$ denotes the exact ground state energy within the given basis set. Additionally, we conduct numerical simulations with tunable noise parameters to identify the dominant sources of noise. We find that orienting the QEC protocols towards higher memory noise protection is the most promising avenue to improve our experimental results.