Victor Armegioiu, Yannick Ramic, Siddhartha Mishra

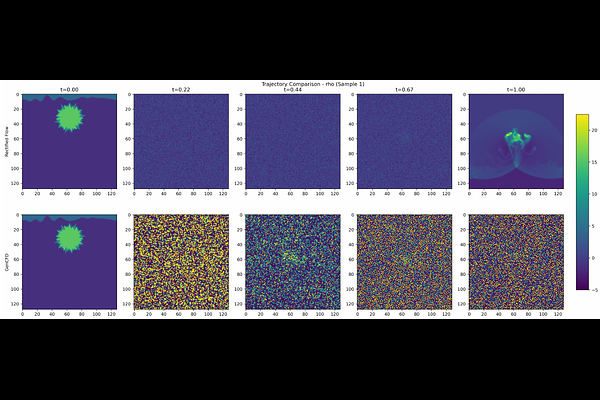
The statistical modeling of fluid flows is very challenging due to their multiscale dynamics and extreme sensitivity to initial conditions. While recently proposed conditional diffusion models achieve high fidelity, they typically require hundreds of stochastic sampling steps at inference. We introduce a rectified flow framework that learns a time-dependent velocity field, transporting input to output distributions along nearly straight trajectories. By casting sampling as solving an ordinary differential equation (ODE) along this straighter flow field, our method makes each integration step much more effective, using as few as eight steps versus (more than) 128 steps in standard score-based diffusion, without sacrificing predictive fidelity. Experiments on challenging multiscale flow benchmarks show that rectified flows recover the same posterior distributions as diffusion models, preserve fine-scale features that MSE-trained baselines miss, and deliver high-resolution samples in a fraction of inference time.