Lan Zhang, Xiang-Xiang Xue, Ling Zhu, Ruizhi Zhang, Chengqun Yang, Shi Shao, Jiang Chang, Feilu Wang, Hao Tian, Gang Zhao, Chao Liu

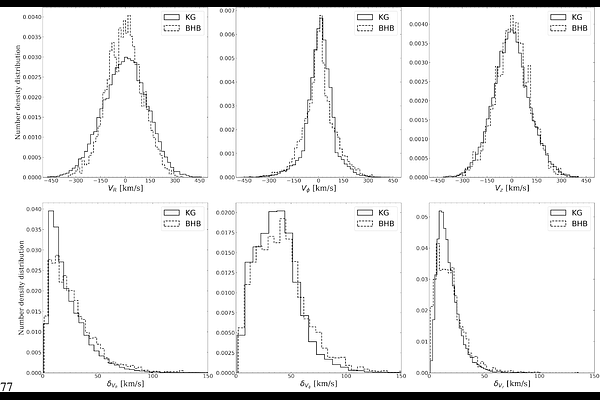
We explore the density profile, shape, and virial mass of the Milky Way's dark matter halo using K giants (KG) from LAMOST and SDSS/SEGUE, as well as blue horizontal branch (BHB) stars from SDSS. Incorporating Gaia DR3 proper motions, we first investigate the velocity ellipsoid distribution within the $(R, |z|)$ space. The ellipsoids projected onto the $(v_R, v_z)$ plane exhibit near-spherical alignment. We then probe the underlying dark matter distribution using the axisymmetric Jeans equations with multi-Gaussian expansion (MGE) and the spherically aligned Jeans anisotropic modelling (JAM${\rm sph}$), allowing for different flattened dark matter density models. For each model, we apply two fitting approaches: fitting the KGs and BHBs separately or fit them simultaneously as two dynamical tracers in one gravitational potential. We find consistent results on the dark matter density profiles, $r_{200}$, and $M_{200}$ within a 1-$\sigma$ confidence region for models constrained by KGs, BHBs, and both. We find the strongest consistency between KGs and BHBs in constraining dark matter profiles for models incorporating radially varying halo flattening ($q(r_{\rm gc})$), which suggests the Milky Way's dark matter halo shape evolves with Galactocentric distance ($r_{\rm gc}$). Specifically, the halo flattening parameter $q_h$ decreases within $r_{\rm gc} < 20$ kpc and increases for $r_{\rm gc} > 20$ kpc. In this model, $M_{\rm tot} (< 60~{\rm kpc}) = 0.533^{+0.061}_{-0.054} \times 10^{12}$ $M_{\odot}$, $r_{200}$ is $188\pm15$ kpc, with $M_{200}$ estimated at $0.820^{+0.210}_{-0.186} \times 10^{12} M_{\odot}$.