Sing Lam Wong, Andrew C. Potter

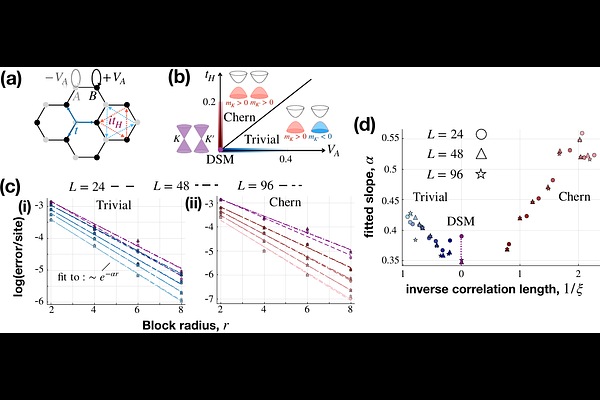
The simulation of entangled ground-states of quantum materials remains challenging for classical computational methods in more than one spatial dimension, and is a prime target for quantum computational advantage. To this end, an important goal is to identify efficient quantum state preparation protocols that minimize the physical qubit number and circuit depth resources required to capture higher-dimensional quantum correlations. This work introduces a quantum circuit compression algorithm for Gaussian fermion states based on the multi-scale entanglement renormalization ansatz (MERA), which provides an exponential reduction in the circuit depth required to approximate highly-entangled ground-states relevant for quantum materials simulations. The algorithm, termed two-dimensional Gaussian MERA ($2d$ GMERA), extends MERA techniques to compress higher-dimensional Gaussian states. Through numerical simulations of the Haldane model on a honeycomb lattice, the method is shown to accurately capture area-law entangled states including topologically trivial insulators, Chern insulators, and critical Dirac semimetals. While Gaussian states alone are classically simulable, this approach establishes empirical upper bounds on quantum resources needed to prepare free fermion states that are adiabatically connected to correlated ground states, providing guidance for implementing these protocols on near-term quantum devices and offering a foundation for simulating more complex quantum materials. Finally, we develop a novel fermion-to-qubit encoding scheme, based on an expanding $2d$ topological order, that enables implementing fermionic rotations via qubit Pauli rotations with constant Pauli weight independent of system size.