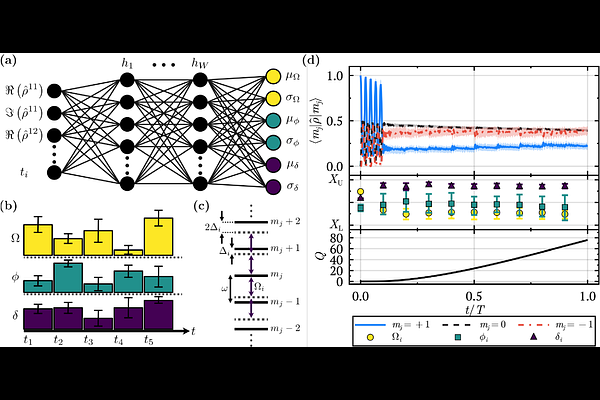
Logan W. Cooke, Stefanie Czischek

Quantum optimal control in the presence of decoherence is difficult, particularly when not all Hamiltonian parameters are known precisely, as in quantum sensing applications. In this context, maximizing the sensitivity of the system is the objective, for which the optimal target state or unitary transformations are unknown, especially in the case of multi-parameter estimation. Here, we investigate the use of reinforcement learning (RL), specifically the soft actor-critic (SAC) algorithm, for problems in quantum optimal control. We adopt a spin-based magnetometer as a benchmarking system for the efficacy of the SAC algorithm. In such systems, the magnitude of a background magnetic field acting on a spin can be determined via projective measurements. The precision of the determined magnitude can be optimized by applying pulses of transverse fields with different strengths. We train an RL agent on numerical simulations of the spin system to determine a transverse-field pulse sequence that optimizes the precision and compare it to existing sensing strategies. We evaluate the agent's performance against various Hamiltonian parameters, including values not seen in training, to investigate the agent's ability to generalize to different situations. We find that the RL agents are sensitive to certain parameters of the system, such as the pulse duration and the purity of the initial state, but overall are able to generalize well, supporting the use of RL in quantum optimal control settings.