W. Leone, L. Burderi, T. di Salvo, A. Anitra, A. Sanna, A. Riggio, R. Iaria, F. Fiore, F. Longo, M. Ďurišková, A. Tsvetkova, C. Maraventano, C. Miceli

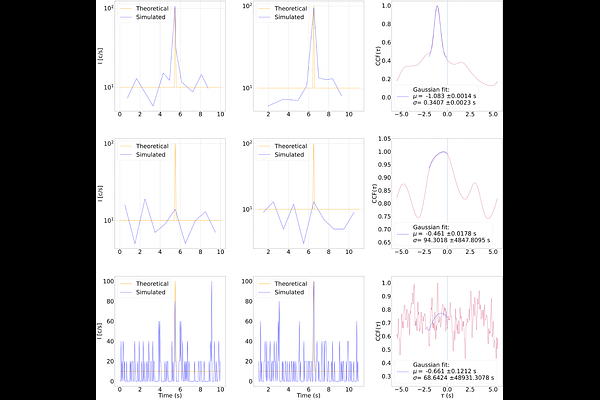
The timing analysis of transient events allows for investigating numerous still open areas of modern astrophysics. The article explores all the mathematical and physical tools required to estimate delays and associated errors between two Times of Arrival (ToA) lists, by exploiting Cross Correlation Function (CCF) techniques. The CCF permits the establishment of the delay between two observed signals and is defined on two continuous functions. A detector does not directly measure the intensity of the electromagnetic signal (interacting with its material) but rather detects each photon ToA through a probabilistic process. Since the CCF is defined on continuous functions, the crucial step is to obtain a continuous rate curve from a list of ToA. This step is treated in the article and the constructed rate functions are light curves that are continuous functions. This allows, in principle, the estimation of delays with any desired resolution. Due to the statistical nature of the measurement process, two independent detections of the same signal yield different photon times. Consequently, light curves derived from these lists differ due to Poisson fluctuations, leading the CCF between them to fluctuate around the true theoretical delay. This article describes a Monte Carlo technique that enables reliable delay estimation by providing a robust measure of the uncertainties induced by Poissonian fluctuations. GRB data are considered as they offer optimal test cases for the proposed techniques. The developed techniques provides a significant computational advantage and are useful analyzing of data characterized by low-count statistics (i.e., low photon count rates in c/s), as they allow overcoming the limitations associated with traditional fixed bin-size methods.