Hou, Z.; Ochoa, A.

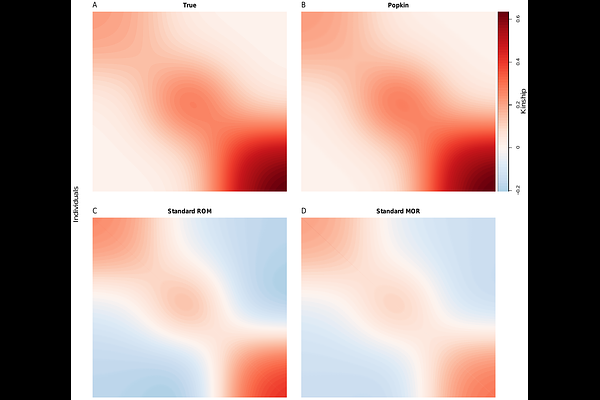
Heritability is a fundamental parameter of diseases and other traits, quantifying the contribution of genetics to that trait. Kinship matrices, also known as Genetic Relatedness Matrices or \"GRMs\", are required for heritability estimation with variance components models. However, the most common \"standard\" kinship estimator employed by GCTA and other approaches, can be severely biased in structured populations. In this study, we characterize heritability estimation biases in GCTA due to kinship estimation biases under population structure. For the standard ratio-of-means (ROM) kinship estimator, we derive a closed-form expression for heritability bias given by the mean kinship value and the true heritability. The standard mean-of-ratios (MOR) estimator is the most widely used in practice, and exhibits more severe bias than ROM due to upweighing low-frequency variants. Using simulation studies with admixture and family structures, as well as simulated traits from 1000 Genomes genotypes, we find that only Popkin, which is the only unbiased population kinship estimator, produces unbiased heritability estimates in structured settings. Pedigree-only estimates have upward heritability biases when there is population structure. Finally, we analyze three structured datasets with real phenotypes---the San Antonio Family Study, the Hispanic Community Health Study / Study of Latinos, and a multiethnic Nephrotic Syndrome cohort. The standard MOR estimator can produce both downward and upward heritability biases depending on population structure and variant frequency spectrum, compared to the other two estimators. Overall, common kinship estimators result in heritability estimation biases when applied to structured populations, a challenge that Popkin successfully overcomes.