Banerjee, S.; Stam, C.; Tward, D. J.; Savoia, S.; Wang, Y.; Mitra, P. P.

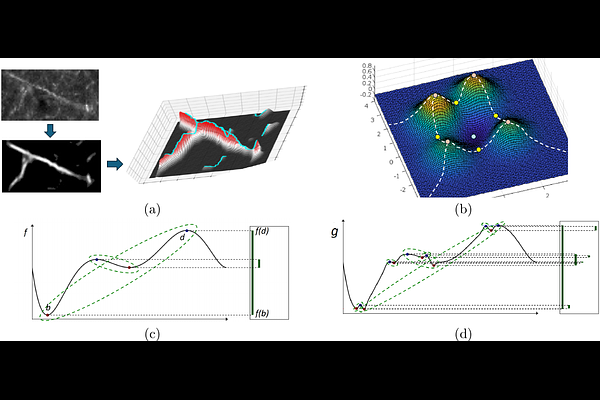
To understand biological intelligence we need to map neuronal networks in vertebrate brains. Mapping mesoscale neural circuitry is done using injections of tracers that label groups of neurons whose axons project to different brain regions. Since many neurons are labeled, it is difficult to follow individual axons. Previous approaches have instead quantified the regional projections using the total label intensity within a region. However, such a quantification is not biologically meaningful. We propose a new approach better connected to the underlying neurons by skeletonizing labeled axon fragments and then estimating a volumetric length density. Our approach uses a combination of deep nets and the Discrete Morse (DM) technique from computational topology. This technique takes into account nonlocal connectivity information and therefore provides noise-robustness. We demonstrate the utility and scalability of the approach on whole-brain tracer injected data. We also define and illustrate an information theoretic measure that quantifies the additional information obtained, compared to the skeletonized tracer injection fragments, when individual axon morphologies are available. Our approach is the first application of the DM technique to computational neuroanatomy. It can help bridge between single-axon skeletons and tracer injections, two important data types in mapping neural networks in vertebrates.