Hinrichsen, R. A.

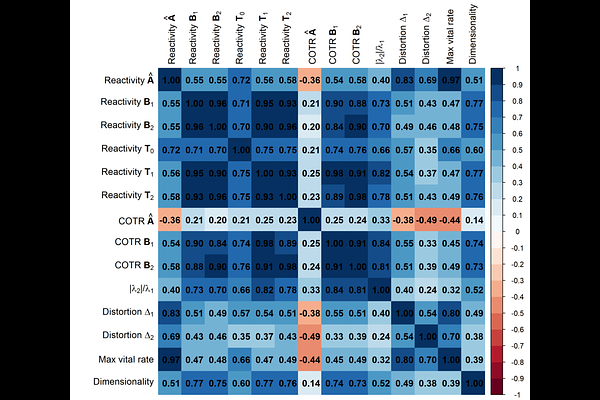
1. Populations are at the mercy of random disturbances large and small and rarely, if ever, converge on predicted long-term behaviours. Therefore, when using matrix population models, ecologists study the dynamics of populations that depart from stable distributions. Necessary for such studies are indices that gauge transient dynamics, which are short-term population fluctuations away from asymptotic trajectories. Conventional indices of transient dynamics present three core challenges: they are distorted by abundant stages of low value (usually immature stages), they are scale dependent, and they conflate transient and asymptotic responses. 2. I develop a new analytical framework for transient dynamics that overcomes these challenges. To solve distortion and scale dependence, I balance a population projection matrix (PPM) by its reproductive values (\'Fisher balancing\') or, alternatively, its stable stage distribution (\'Demetrius balancing\'). To disentangle transient and asymptotic dynamics, I strip a PPM of its output in the direction of its stable stage distribution, resulting in a \'transient\' PPM. I develop indices of transient dynamics that gauge the \'size\' of a transient PPM using reactivities defined by matrix norms. Among these indices is a new \'coefficient of transient response\' (COTR) that represents the fraction of the sum of squares of the total response that is explained by the transient response. In addition to the indices of transient dynamics that apply directly to PPMs, the framework also includes case-specific indices of transient dynamics that arise from a specified initial stage vector. 3. Using a dataset of 6,332 PPMs retrieved from the COMPADRE Plant Matrix Database, I compared the new analytical framework with the conventional framework without balancing, focusing mainly on transient responses estimated by COTR. The new framework dramatically changed the rankings of PPMs from the least to the greatest transient dynamics. Spearman correlation between COTR of standardised PPMs and that of balanced PPMs was weak (less than or equal to 0.25). This change in rankings led to new inferences about which taxonomic orders were least or most prone to transient dynamics. 4. By solving three core challenges, the new framework produces a clearer and more robust portrait of transient dynamics.